一个简单的克莱因瓶，为什么穷尽科技都无法制造？差了一维空间

克莱因瓶是一种数学上的概念，它是一种不可定向的二维紧致流形，也就是说，它是一个没有边界、没有内外之分、只有一个面的曲面。它的名字来源于德国数学家菲利克斯·克莱因，他在1882年提出了这个概念，试图用它来描述四维空间中的物体。克莱因瓶的构造方法是把一个圆柱体的两个底面粘合在一起，但是在粘合之前，要把其中一个底面旋转180度，这样就会形成一个自相交的曲面，从图中可以看出，克莱因瓶的瓶颈和瓶身并不是真的相交，而是在四维空间中通过第四维连接在一起的，所以在三维空间中看起来才会有自交的假象。这就是克莱因瓶的奥妙之处，它是一个四维空间中的物体，而不是一个三维空间中的物体。

影响

克莱因瓶作为一个数学上的概念，它对数学的发展和应用有着重要的影响。它是拓扑学的一个基本对象，拓扑学是一门研究空间形状和变化的数学分支，它关注的是空间的性质和结构，而不是空间的度量和距离。拓扑学的一个核心思想是连续变形，也就是说，如果一个空间可以通过拉伸、扭曲、压缩等方式，而不断开或粘合，变成另一个空间，那么这两个空间就是拓扑等价的，它们有着相同的拓扑性质。比如，一个圆环和一个方形是拓扑等价的，因为它们都是一个没有边界的闭合曲线，可以通过拉伸和扭曲变成对方的形状。而一个圆环和一个克莱因瓶就不是拓扑等价的，因为它们有着不同的拓扑性质，比如，圆环是可定向的，而克莱因瓶是不可定向的，这一点无论如何变形都无法改变。

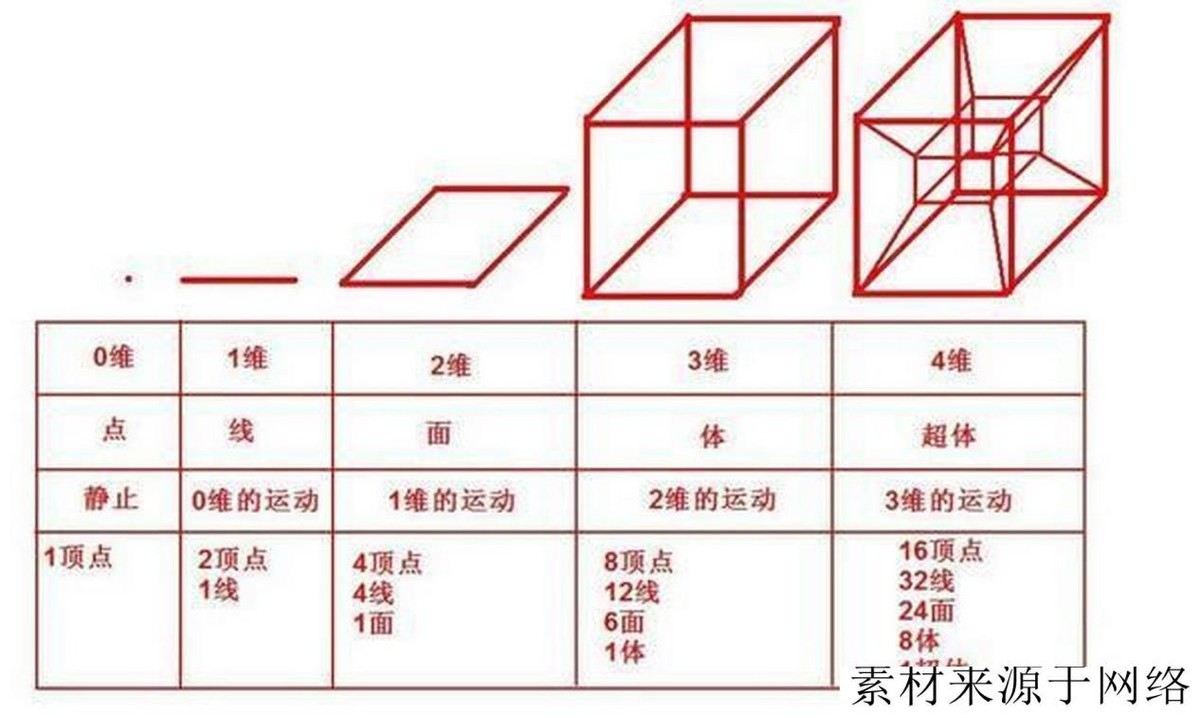
拓扑学的研究对于理解空间的本质和结构有着重要的意义，它可以帮助我们发现空间的一些隐藏的规律和奇妙的现象，比如，克莱因瓶就是一个展示了四维空间的可能性的例子，它让我们意识到，我们所生活的三维空间并不是唯一的，还有更高维的空间存在，而且这些空间可能有着我们难以想象的性质和结构。拓扑学的研究也对于其他数学领域和自然科学领域有着广泛的应用，比如，代数拓扑学可以用代数的方法来描述和分类拓扑空间，微分拓扑学可以用微积分的方法来研究拓扑空间的局部性质，几何拓扑学可以用几何的方法来研究拓扑空间的整体性质，拓扑动力学可以用拓扑的方法来研究动力系统的行为和稳定性，拓扑数据分析可以用拓扑的方法来分析和可视化复杂的数据结构，拓扑量子场论可以用拓扑的方法来描述和计算量子物理中的场和粒子的相互作用，等等。

意见

克莱因瓶是一个简单而又复杂的概念，它是一个无法在三维空间中制造的物体，因为它差了一维空间。它是一个挑战我们对空间的认知和想象的物体，因为它有着我们无法直观理解的性质和结构。它是一个启发我们对空间的探索和创造的物体，因为它展示了空间的多样性和可能性。它是一个连接数学和自然科学的物体，因为它是拓扑学的一个基本对象，而拓扑学是一门有着丰富的理论和应用的数学分支。总之，克莱因瓶是一个值得我们深入学习和欣赏的物体，它是一个数学上的美妙之作，也是一个自然界的奇迹之作。