一般系统伯德图作图方法

系统幅频特性的伯德图可由各典型环节的幅频特性伯德图叠加得到。

同理，系统相频特性的伯德图亦可用各典型环节的相频特性伯德图叠加得到。

对一般系统

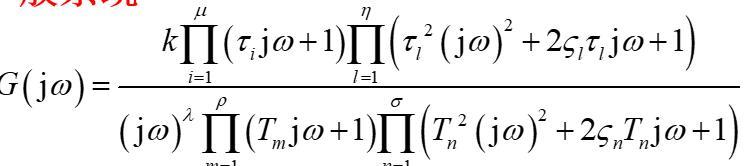
则

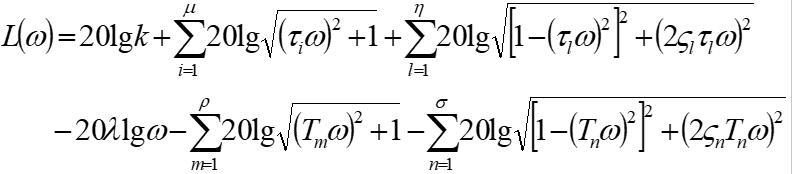
伯德图可由如下步骤形成：

(1)将系统频率特性化为典型环节频率特性的乘积;

(2)根据组成系统的各典型环节确定转角频率及相应斜率，并画近似幅频折线和相频曲线;

(3)必要时对近似曲线作适当修正。

真正画伯德图时，并不需要先画出各环节伯德图，可根据静态放大倍数和各环节时间常数直接画出整个系统伯德图。

系统开环传递函数在 S右半平面上既无极点、又无零点的系统，称为最小相位系统；否则，为非最小相位系统。对于相同阶次的基本环节，当频率W从0变到正无穷时，最小相位的基本环节造成的相移是最小的。

最小相位系统的相频特性和幅频特性是一一对应的，知道了系统幅频特性，其相频特性就唯一确定。

许多系统的物理模型很难抽象得很准确，其传递函数很难用纯数学分析的方法求出。对于这类系统，可以通过实验测出系统的频率特性曲线，进而求出系统的传递函数。

由伯德图的作图过程可知，幅频曲线的转折点对应的频率是时间常数的倒数。

翻译成英文：

General system Bode diagram drawing method

The Bode diagram of the amplitude-frequency characteristics of the system can be obtained by superposing the Bode diagrams of the amplitude-frequency characteristics of each typical link.

In the same way, the Bode diagram of the phase-frequency characteristics of the system can also be obtained by superimposing the Bode diagrams of the phase-frequency characteristics of each typical link.

For general system

The Bode diagram can be formed by the following steps:

(1) Convert the system frequency characteristics into the product of the frequency characteristics of typical links;

(2) Determine the corner frequency and corresponding slope according to the typical links that make up the system, and draw approximate amplitude-frequency fold lines and phase-frequency curves;

(3) Make appropriate corrections to the approximate curve when necessary.

When actually drawing the Bode diagram, it is not necessary to draw the Bode diagram of each link first.

The Bode diagram of the entire system can be drawn directly according to the static magnification and the time constant of each link.

The system in which the open-loop transfer function of the system has neither poles nor zeros on the right half plane of S is called a minimum phase system; otherwise, it is a non-minimum phase system.

For the basic link of the same order, when the frequency W changes from 0 to positive infinity, the phase shift caused by the minimum phase basic link is the smallest.

The phase-frequency characteristics and amplitude-frequency characteristics of the minimum phase system correspond one-to-one.

Knowing the system's amplitude-frequency characteristics, its phase-frequency characteristics can be uniquely determined.

It is difficult to abstract the physical model of many systems very accurately, and its transfer function is difficult to obtain by pure mathematical analysis.

For this type of system, the frequency characteristic curve of the system can be measured through experiments, and then the transfer function of the system can be calculated.

It can be seen from the drawing process of the Bode diagram that the frequency corresponding to the turning point of the amplitude-frequency curve is the reciprocal of the time constant.

参考资料：清华大学控制过程基础PPT

英文翻译：Google翻译

本文由learningyard学苑原创，部分资料、图片来源于网络，如有侵权请联系。